重回帰分析は数量データを使って、例えば総合評価に影響する詳細項目の影響度を測ったり、売上げ予測モデル式を作成する手法です。
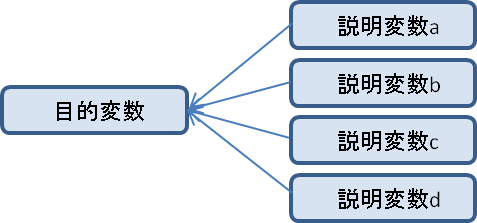
重回帰分析では総合評価や売上げを目的変数、総合評価を決める元となる詳細項目や、売上げを決める元となるデータ、販売日数、売り場面積、来店者数などを説明変数と呼び、目的変数と複数の説明変数との関係を求め、説明変数から目的変数を推定します。
重回帰分析の説明変数
重回帰分析の説明変数は数量データ。
質的データ(性別など数量でないカテゴリーデータ)の場合は数量化Ⅰ類を用います。
調査応用例
商品の売上げに寄与する要因分析、売上げ予測
商品の保有に寄与する要因分析
広告認知に寄与する要因分析
総合満足評価に対する詳細項目の寄与度分析 等
説明変数の選択
重回帰分析は、説明力が高い、なるべく少数の説明変数で、適合度の高いモデル式を作ることが理想とされています。
説明変数は以下の方法によって、最終的な説明変数を決めていきます。
強制投入法:すべての変数を説明変数として重回帰式を作る。
変数増加法:既存の重回帰式に、新たな変数を追加しては、評価していく。
変数減少法:既存の重回帰式から、1つずつ変数を減少させて、評価していく。
ステップワイズ法:説明変数を1つずつ入れたり抜いたりしながら、だんだんとあてはまりのよいモデルに近づけていく。
多重共線性(マルチコ)
重回帰分析の説明変数同士は、相関が低く独立していなけばなりません。
説明変数A、B間に相関が高いと、目的変数に対するAの寄与度とBの寄与度を分けることができず、適切な偏回帰係数が求められません。
これを、多重共線性(マルチコリニアリティ)といいます。
多重共線性があると、本来目的変数にプラスに寄与する項目が、マイナスの寄与率となってしまうなどの現象が起こります。多重共線性は説明変数間の相関行列を調べることで発見し、相関の高い説明変数を落とします。
事例1
[解析目的]
スクーターの総合満足度評価及び、信頼性、価格などの詳細項目の評価についてのユーザーの回答結果から、総合満足度評価を上げるために、重要な要素、改善のための重点ポイントを探るため、各項目の評価得点をもとに重回帰分析を行った。
[解析方法]
目的変数、説明変数を下記とする重回帰分析を実施。
目的変数-総合評価
説明変数

[解析結果]
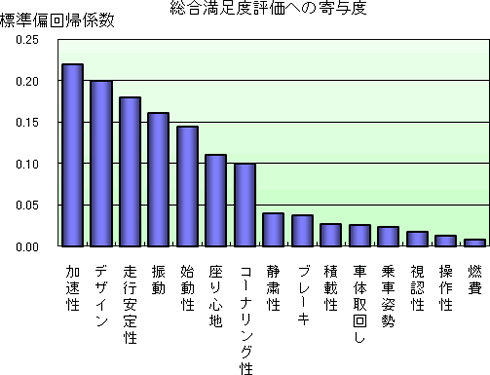
満足度評価への寄与度(影響の強さ)は「加速性」「デザイン」「走行安定性」「振動」「始動性」などが高く、これらの評価を高めることが総合的な満足度を上げるために最も効果がある。
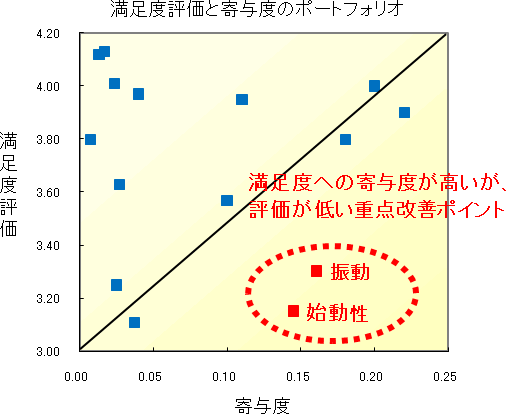
満足度評価と寄与度の関係をみると、「振動」「始動性」は寄与度が高いにも拘らず、満足度が低く、この2点が改善のための最重要ポイントとして浮かび上がる。