コンジョイント分析を行うと概ね個別効用値と言って、各対象者ごとの各属性の各水準に対する効き目具体の数値が求められることは説明しました。

効用値には、離散水準と線形水準、つまりディスクリートとリニアという二つのデータタイプが存在します。

ディスクリート（離散）は、色やデザインなど順位が付けられない、大小の比較ができない水準です。青と赤どちらが優位か、どちらが高いかなどは言えません。

これに対し、リニア（線形）では、これが言えます。例えば価格です。

5000円は6000円より効用が高い。これは当たり前のように言えることです。5000円と6000円の間は5500円である。これも言えます。

このリニア（線形）水準の時に、実際の調査では提示されていなかった間の水準を仮想的に想定し、その効用値を求めることが可能です。

これをpolationと読んでいるようです。

提示した金額などの水準をknown-points、そして5000円と6000円の間の5500円など実際には対象者に提示されていない金額などの水準をunknown-pointsと呼びます。

known-pointsはまさに対象者が回答中に見た、金額などの水準です。（我々が設定した水準です）
これに対しunknown-pointsは特定の水準間の中央値など実際に提示されたことがない仮想水準です。

効用値はknown-pointsに対して算出されます。unknown-pointsはknown-pointsから推計（直線回帰）されます。二点間の回帰線上のポイントとして比率を考慮し求められます。

非常に単純です。

ちなみに、Sawtooth社の扱っているコンジョイントツールでは、通常、効用値の多くは属性内の各水準の効用値の合計は0になるように再計算されています。

これは属性間での効用値比較をするという間違いを防ぐ目的で0点から両側に効用値を配分しているためです。

しかし、unknown-pointsで算出された効用値の場合、属性内で何をたしても合計値が0にはなりません。
効用値はknown-pointsに対して算出されます。unknown-pointsはknown-pointsから推計（直線回帰）されますので、 unknown-pointsはknown-pointsの存在が前提となります。つまり、新たなknown-pointsを考慮して属性内合計を0にしてしまうと元々の効用値がおかしくなってしまいます。

polationでは、二点間の外側に位置するunknown-pointsも求めることは可能です。

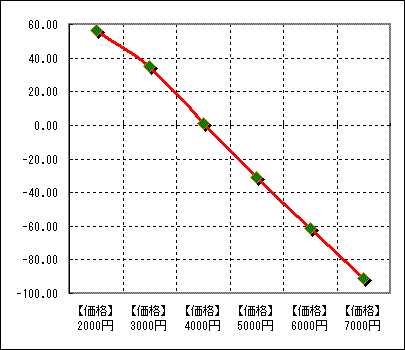
例えば、提示された水準が1000円、2000円、3000円、4000円、5000円、6000円までだったとしましょう。
この場合7000円は外側に位置します。シミュレーション上では実はこの7000円という外側も指定してシミュレーションを実施することが可能です。

直近の二点間からの延長線を引き、その上に7000円などの点を作り、効用値を求める計算をシミュレータの内部で行います。

ちなみに水準間の内側の中間等の部位に位置する仮想水準を求めることをInterpolationと言います、これに対し今回のように7000円など水準外にある仮想水準を求めることをExtrapolationと呼んで区別しています。

Interpolationは実際に提示されているknown-pointsの2点間の間に入りますので、推計値は必ずknown-pointsの間に存在します。これは信頼性としては高いと言えます。